解决问题是小学数学教学中的一个难点。在实际教学中,教师如果不注重方法,就会收效甚微,在讲授中高年级复杂的数量关系问题时尤其如此。下面,我就小学数学解决问题教学简单谈一些自己的做法和体会。
一、学会审题是关键
审清题意,是解决问题教学的关键。在教学中,可告诫学生拿到试题后先别着急做,要先根据题意找出题目中的直接条件和间接条件,明确数量关系。同时,为了便于分析已知量和未知量之间的相互关系,在审题时要求学生边读题边思考,标出题目中的已知条件和问题,或用线段图表示。
为使学生养成仔细审题的习惯,我在出题时经常把一些容易混淆的题目交织在一起,让学生分析计算。例如:(1)运输公司有客车与货车共250辆,客车是货车的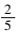 ,有客车多少辆?(2)运输公司有货车250辆,客车是货车的
,有客车多少辆?(2)运输公司有货车250辆,客车是货车的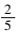 ,有客车多少辆?题(1)中250辆为共有的数,题(2)中250辆是其中一种,因此计算方法不同。经常进行这种练习,学生就很容易养成仔细审题的习惯。
,有客车多少辆?题(1)中250辆为共有的数,题(2)中250辆是其中一种,因此计算方法不同。经常进行这种练习,学生就很容易养成仔细审题的习惯。
二、教给学生正确的解题方法
在平时做题时,有些学生不会认真思考,只会机械模仿教师讲解的方法,碰到正好适合的题目,自然能够迎刃而解,但是题目如果稍微发生变化,就又不知该如何化解。因此,教师要教给学生正确的分析方法。目前,分析法和综合法是常用的方法。分析法,简单说就是从问题开始,由后往前,逐步分析。首先思考,要解决问题需要哪些条件,这些条件哪些是已知的,哪些是未知的。直到未知条件都能找到为止。
例如:小刚今天卖蔬菜30千克,小红比小刚多卖15千克,两人一共卖多少千克?指导学生分析:要求两人一共卖多少千克,必须要知道哪两个已知条件(小刚卖的和小红卖的)。题中给出的条件哪个是已知的(小刚卖的),哪个是未知的(小红卖的),应先求什么(小红卖的,30+15=45),然后再求什么(两人一共卖多少千克,30+45=75)。
综合法是从题目的已知条件出发,通过分析推出题目中要求的问题。如上例,可以让学生这样想:已知小刚卖了30千克,小红比小刚多卖15千克,就可以求出小红卖的(30+15=45),然后就能求出两人一共卖的(30+45=75)。
通过上面的两种解题方法可以得出,不管是用分析法还是综合法,都是把已知条件和要求问题结合起来考虑,最后要求的问题是思考方向,已知条件就是解题的条件。
三、角色互换,让“兵”教“兵”
在讲授解决问题这类题目时,教师总认为自己给学生分析得非常透彻,但仍有部分学生始终不能理解,这其实不能怪学生基础掌握得不扎实或者学生智力问题。这时,不妨变通一下思路,让“兵”教“兵”,就是让学生教学生——有时候,学生的语言能够超越教师的语言,他们有比教师更通俗的讲解方式。通常,学生列出算式后,我都要求学生把每一步的想法和依据介绍给大家,力争让所有学生都能听明白。这样做既可以提高课堂教学效率,又可以培养学生的表达能力,还能进一步拓展学生的思维和知识。
四、注重自编解决问题的训练
让学生会解这种类型的题目,首先要让学生了解这类题型的结构,教师要重视学生自编问题的教学,这是提高学生解题能力的重要一步。因此,在低年级教学时,就要让学生了解一道题是由已知条件和所求问题两部分组成的,可进行填空练习。例如:公园有杨树100棵,桐树比杨树多35棵,桐树有_____棵?到了高年级,要引导学生通过自编问题,认识和掌握各类这种题目的结构特点。(1)根据算式编题:180×_____=_____?编一道解决问题的题目。(2)把一种说法换成另一种说法的题目:例如我有48元钱,花了_____,花了_____钱?把它变成一道已知一个数的几分之几是多少,求这个数的问题。(3)指定类型编题,例如编反比例解决问题的题等。通过这些训练,让学生熟练掌握这种类型题目中各部分之间的关系,为今后解题打下良好的基础。
提高学生解答这种题型的能力需要长期不间断地对学生进行培养,只要我们重视,再加上科学的方法做指导,学生解题能力一定会有大的提高。


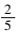 ,有客车多少辆?(2)运输公司有货车250辆,客车是货车的
,有客车多少辆?(2)运输公司有货车250辆,客车是货车的