在数学课堂教学中,教师强调发散学生的思维,鼓励学生思维的求异性,往往是用一题多解或通过比较不同问题的相似解法来达到这一目的,但在教学过程中却常常只是简单的让学生把自己的想法一一罗列。至于为什么可以这样想,哪些想法是他们理解的,哪些是不理解的,教师并不是很清楚。笔者以为,在新课程改革理念下的数学教学过程中,解决问题活动的价值不局限于获得具体问题的结论和答案,它的意义更在于使学生经历探索解决问题策略的途径和过程,学会解决问题,体会每个人都应当有自己对数学问题的理解和解决方案,并由此形成自己解决问题的基本策略、最优策略,并体验解决问题策略多样性的乐趣。只有在这种鼓励个性发展的理念下进行数学教学,学生的创新精神才可能真正得到培养。
一、在计算中体会
小学数学教学培养学生的计算能力是准确、迅速和灵活。由于学生生活背景和思考角度不同,所使用的方法必然也是多样的。教学中,教师要尊重学生的想法,鼓励学生独立思考,提倡计算方法的多样化。
国标本苏教版二年级上册数学教材中,“65+28”的教学:
教师出示问题并提问:“同学们,你打算怎样计算它呢?看谁能想出好的计算方法?”然后,给学生充足的时间独立思考。
学生交流自己的想法,教师板书列出:

在学生的交流中,教师问学生:“你是怎样想的?刚才你是怎样做的?你还有不同的算法吗?别人的方法是怎样的?你认为哪种方法好?更适合你?”教师不要急于评价各种算法,而应该不断加以鼓励,让学生自己通过对比、研究不同算法的特点,选择适合自己的方法、最优的方法。通过这样的学习、讨论,每个学生都能在不同的算法中找到最适合自已的计算方法,丰富自己的思维,从而体会到解决问题策略的多样化。
二、在交流中体会
数学教学要促进学生个性化发展,允许不同的学生从不同的角度去认识问题、采用不同的方法来表达自己的想法、用不同的知识内容和方法去解决问题,发展学生的发散思维能力,使学生在更多、更主动的同伴交流中,发表自己的观点,倾听同伴的解法,体验解决问题策略的多样性。
国标本苏教版数学第九册中,“解决问题的策略”的教学:王大叔用18根1米长的栅栏围成一个长方形羊圈,有多少种不同的围法?
让学生理解题意后,教师放手让学生在学习小组里共同研究如何解决这一问题的方法。
方法一:动手摆一摆。
学生演示摆的方法:长方形的宽摆一根小棒,宽就可以看成是1米,长就是8米;如果长方形宽摆2根小棒,宽就可以看成是2米,长就是7米……
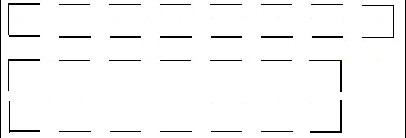
方法二:动手画一画。
如果画的长方形的宽是1米,那么长就是8米;如果画的长方形的宽是2米,那么长就是7米……
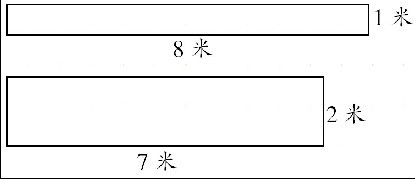
方法三:列表整理。
先根据题意计算出围成的长方形长与宽的和,再列表。
18÷2=9(米)

这样,学生在小组充分讨论的基础上体会到同一问题的不同解决途径。在这样的学习过程中,每一位学生都经历了思考的过程,经历了解决问题的不同途径。学生对不同方法进行分析、讨论、比较,能够吸取不同方法的精华,悟出属于自己的解决数学问题的最优策略,体验了解决问题的策略多样化。
三、在实践中体会
解决数学问题其实就是一种数学实践活动,是培养学生进行主动探索与合作交流的重要途径。在教学中,通过学生已有的生活背景材料,运用已有的数学知识,及时引导学生将所学习的知识运用到生活实际中去,从而在解决实际的问题中体验解决问题策略的多样化。
课堂上教师除了努力为学生应用所学知识去解决问题创造条件和机会之外,还应鼓励学生自己主动在现实中寻找用数学知识和数学思想方法解决问题的机会,并努力去实践。面对现实问题,学生能够主动从数学的角度进行分析并探索解决方案,也是数学教学中培养学生问题解决意识的根本所在。
国标本苏教版数学第七册中, “找规律”的教学出示数学问题:

问:如果每两棵树之间的距离是20米,那么这条路一共有多少米?
学生根据图意很快列式计算:20×5=100(米)
问:算式中的“5”是怎样得到的?学生回答:数出来的。
师:如果这里的树有300棵,你也会像刚才那样数吗?有什么好的方法?
如果有300棵树,只有一端栽树,这条路有多长呢?

如果有300棵树,而两端都不栽树,又该如何思考呢?

请同学们想一想,在你们的生活中有没有类似的现象或例子?启发学生留心回忆、联想再现生活中一些类似的情况,想想其中的规律,试着去解决这几个问题。
学生思考后,让学生讨论,在交流中使学生体会到我们生活中道路两旁的行道树、路灯、校园里摆放的盆花等等都有着类似的现象(出示路旁的行道树、路灯及校园里走廊上摆放的盆花图片等等)。教师边演示,边有意识地让学生数一数,算一算。在此基础上再让学生独立思考,从而发现解决这一问题主要是要找到棵数与分成的段数之间的联系,找到它们之间的内在规律,问题就迎刃而解了。在这一过程中教师主要是让学生去联想再现体验生活中的实例,联系生活中去感知,并在此基础上帮助学生得出棵数、段数及路长之间的关系。
当然,教师在教学中要引导学生注意观察的选择性、灵活性、准确性、目的性与完备性。用生活中的实例帮助自己去寻找解决相同问题的不同方法及解决相似问题的不同方法。
教师要在解决问题方法的多样化中,去鼓励、启发学生积极思考,并尊重学生的独立思考;让学生在探索不同的解题方法中、在师生和同伴的相互探究、交流讨论与启发中理解、体验用多种方法去解决同一个问题,并逐步掌握解决问题的最优策略,从而让不同的知识背景和思考角度的学生都能得到有效地发展。








