波利亚指出：“只要数学的学习过程能反映数学的发明过程的话，那么就应该让合理的猜测占有适当的位置。”因此在教学过程中要十分重视让学生大胆猜测、动手实践。
     下面是《圆的面积》教学的一个环节：
师：同学们，你们使用过哪些方法探究长方形、平行四边形、梯形、三角形的面积计算方法？
生1：用数方格的方法知道了长方形的面积可以用长乘宽计算得到。
生2：在研究三角形和梯形的面积计算方法时已经不用数格子的方法了，用拼平行四边形的方法进行探究。
师：通过测量相关条件，计算得到的图形面积才是比较精确的。面对这样一个圆，你又有什么猜想呢？
生1：是否也能用割补的方法把这个圆转化成刚才的那些图形？
生2：圆是曲线状，两个圆拼不出基本图形，只能分割了。分割成什么样的图形？然后拼成什么样的图形？请大家帮我想办法。
生3：应该可以转化的，怎么分是关键。
师：真聪明，为你们自豪。分割成什么图形呢，我们共同出谋划策吧。
师：如果让你从长方形、平行四边形、三角形、梯形中挑选一种图形做拼图试验，你将选择哪一个？
生1：选长方形，拼和算都方便。
生2：选平行四边形，有尖角。长方形只有直角，难变化。
生3：我选三角形，因为三角形可以拼成这几个中的任何一个图形。
师：你真棒！那圆形如何分割成三角形呢？不可能……真的吗？请看钟面。
师：除了有圆这个封闭图形外，能借助想象力再找个封闭图形吗？
生1：如果把时针和分针延长到钟的边上就是扇形了。教师出示准备好的图形：

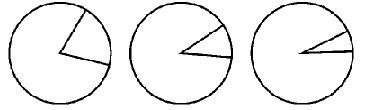
生2：有“三角形”了。那个小扇形可以看作近似的三角形。扇形越小越接近三角形。
生3：分的份数越多，那弯的一条边拼在一起就越接近直线。
师：表述得很清晰，能证实一下吗？试一试。

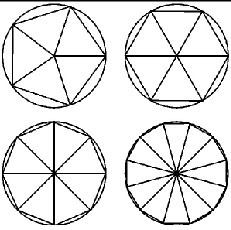
     接着小组间猜一猜、画一画、剪一剪，证实了猜测。“三角形”使探究的瓶颈被突破了，学生探索的情绪一下就高涨了。接着小组合作顺利得到圆面积的计算方法。
     《圆的面积》传统的教法是：从4等份拼成的不规则图形到32等份能拼成的一个近似长方形，从中感悟“极限”。最后得到长方形的长等于圆周长的一半，宽就是圆的半径，长方形的面积相当于圆的面积，推导出圆的面积公式。让学生探索的教学过程是对传统教学的突破，关注知识的形成过程，让学生在获得知识与结论的同时培养了学习能力，提升了思维能力。因此，让学生大胆猜测、主动探索，在数学教学中就表现出以下一些优势：
     一、思维发展的深刻性
     知识的本身并不重要，重要的是数学思想和方法，这才是数学的精髓。圆面积教学突破点放在让学生明白“转化”的重要，精彩在于怎样引导学生去“转化”。在学生迷惘时教师运用钟面这一道具，让学生观察，借助想象力发现：两条半径和圆上的一段弧线围成的图近似于三角形，引导学生去思考问题。学生在与同伴的交流过程中领悟“极限”思想，思维在交流中得到启发，并得到发展。
教师面临一个个学生自发生成的问题情境，不急于给出答案，而是适时地让学生思考、讨论，进行大胆的直觉判断和猜想。整个学习过程是“猜想——验证”的过程，是发现问题和解决问题的过程。学生在观察、猜测、操作、验证、归纳的过程中理解数学问题是怎样提出的，结论是怎样得到的。
     二、学习过程的主动性
     引导学生成功地回忆“转化”法，顺势让学生自己提出猜想，产生探究的欲望：“可以用移补的方法吗？”“分割成什么图形？”“圆的面积有计算公式吗？”……充分体现了学生学习的主动性与内驱性。由于问题的驱动，学生的好奇心被充分调动起来，为他们随后展开探究活动作好了铺垫。 学生的一句话“请大家帮我想办法”充分表露了学生的求知欲望。
     三、学习情感的互动性
     曲线围成的圆与三角形缺乏直观联系，在学生迷惘时，老师拨动了时针，学生的思维受到了启发。学生把小扇形想象成“三角形”时，教师及时提出了“你们能证实一下吗”。在学生由感而发产生猜测时，教师由衷地表扬学生“真有智慧，为你们自豪”。整个学习过程中师生相互欣赏，印证了情感与需要具有相互制约的规律。寻求圆面积计算方法的过程与学生主观需要相符合，特别是近似三角形的发现让学生探究的心理得到了满足。