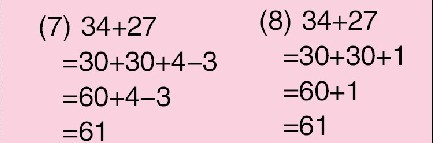数学教学是师生之间、学生之间交往互动与共同发展的过程。由于学生的生活背景和思考角度不同，所使用的方法必然是多样的，教师应尊重学生的想法，鼓励学生独立思考，提倡计算方法的多样化。如对于计算34+27的问题，学生可以采取多种方法，以下列举的方法都应当受到鼓励。

（1）、（2）、（3）、（4）四种方法出自课程标准。在实际教学时，学生又说了方法（5）、（6）
          

根据方法（6），有学生又说出了方法（7）和（8）

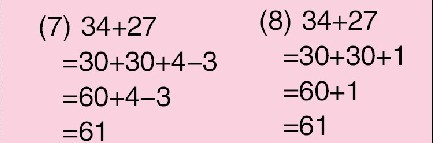
数学课程标准强调，要让学生体验解决问题策略的多样性，了解同一问题可以有不同的解决办法，笔者认为算法多样化并不是让每一位学生掌握每一种方法，而是让个性不同的每一位学生从众多方法中理解、掌握、选取适合自己的方法，但绝不是找出一种看似可能的最好的方法，所以要对不同的算法在不同个体上进行优化。
一、适合自己的才是最好的
计算34+27时，课标上给的只是部分方法；作为教师来说，因为思维定势，头脑里也没有这样的八种方法。学生对于这个新知的学习，首先没有思维定势，因为知识背景不同，思考的角度更不同，算法自然也不同，只要是适合学生自己的方法就是好方法。如使用方法（8）的学生，完全是在理解了方法（7）的基础上，对方法（7）的延伸、归纳（+4-3就是+1），没有人在口算的时候还说出具体的口算过程，能够对具体的口算过程进行个体的加工，才是真正掌握了口算的方法，所以适合自己的才是最好的。
二、适合不同题型的才是最好的
教学苏教版三年级上册《长方形周长计算》时，学生说出了这样几种方法：
方法一：28×2=56  15×2=30
6+30=86
方法二：28+28+15+15=86
方法三：28+15+28+15=86
方法四：28+15=43  43×2=86
课后练习时，教师有意识地设计了这样一组题，看谁算得快：
① 长是99厘米，宽是1厘米，周长是多少厘米？
② 长是50厘米，宽是11厘米，周长是多少厘米？
③ 长是30厘米，宽是20厘米，周长是多少厘米？
“算得快”的要求，让学生有竞争意识，也让学生对计算方法有所选择，因为自己当初喜欢的方法不一定是最快的。
第一个问题出示后，学生居然都选择了方法四。教师追问他们为什么选择方法四？他们一致回答：因为99+1=100，能凑成一个整百数，这样不仅速度快而且肯定是对的，而方法二太麻烦。
第二个问题出示后，大部分学生都选择了方法一。再追问他们为什么不用刚才的方法四了，学生的回答是：“这题和第一题不一样，长和宽相加不能凑成整百数，但是方法一却能将两个长凑成整百数，两个宽相加非常好算。”学生虽然语言质朴，但是已经明白适合不同题目的方法才是最好的方法。
第三题出示后，课堂已经炸开了锅，学生有的说一好，有的说二棒,各有说辞，互不相让，都说自己的方法是最快的。教师又进一步引导：请说说你们各自选的方法好在哪？不同方法之中有相同之处吗？一番激烈争吵和冷静思考之后，学生的回答是：“这一题长和宽都是整十数，不管用那种方法算，都很好算。”
三、适合不同学习阶段的才是最好的
笔者曾经听过一堂学前班学生的速心算课，学生是5岁左右的孩子，内容是“和是十几的加法”，教师教给孩子们的方法是这样的：今天学的都是“和是十几的加法”，看到9，第二个数就减1，第二个数剩几，和就是十几；看到8，第二个数就减2，依次下去。听了这种方法笔者非常吃惊，于是问旁边的孩子学会了吗，孩子边说会，边“刷刷刷”在纸上做完了教师发的作业纸，而且结果都是正确的。再问他看到9为什么要减1时，他的回答是不知道。对于这些孩子来说，他们这堂课掌握的仅仅是速算的技巧，这种技巧很好，但是只是一种单纯的模仿和方法的强行记忆。从学生思维训练的角度来说，笔者不赞同这种技巧的灌输。
笔者认为技巧性的记忆固然重要，但不应该在学习之初就对学生进行灌输。对于低年级甚至更小的孩子们来说，孩子的认知特点应该是一个从具体到抽象的渐进过程，理解基础上的知识掌握才应该是有效的学习方式。就拿“和是十几的加法”来说，笔者设计了这样一个渐进的学习过程：
① 出示一些杂乱的小棒（大约十几根），问学生：这里有多少根小棒？怎样分类才能让人一眼就看出有多少根小棒？此环节设计目的让学生将十个圈成一圈，就能很快数出有多少根小棒。
② 情境教学9+4，把一个大盒子分成十个小格子，里面装有9个桃，盒外有零散的4个桃，问：一共有多少个桃？你是怎样知道的？教师应该允许学生有不同的想法，如一个一个数出来有13个；用小棒摆一摆；因为10+4=14，所以9+4=13；拿一个放在左边的盒子里凑成10个，就能看出有多少个桃……
③ 抽象出9+4的方法并板书，指导学生讨论以上方法的优劣，是否理解，是否是自己喜欢的方法，选择合适的方法计算。在方法的交流中，教师逐步抽象总结出凑十法，把9凑成10，需要将4分成1和3后再计算。
④ 题组练习，找共性，明确把9凑10，只需将第二个数分成1和几后再算。教师此时可以渗透出技巧介绍：看到9，第二个数就减1，并强调地说一说为什么要减1。
⑤ 拓展延伸：出示8+7，让学生说说自己的方法。
教师要在学生不同的学习阶段，采用不同的教学方法：在这个渐进的教学过程中，学生由引入新课时圈十易数，到新课时摆十得出答案，到小结时凑十找共性，到练习时的技巧介绍，再到最后的方法延伸。这其实是对凑十方法的感知、操作、理解、掌握、运用和延伸的学习过程；是在情境教学中，学生参与、自主探索、主动获得解决问题的方法；同时也是对不同层次的方法进行优化，从低级到高级，从具体到抽象的过程引导。这样的安排满足了不同学生的不同学习要求，让不同的人在数学上得到不同的发展。
综上所述，教师在关注算法多样化的同时，更应该关注学生的个体差异，优化出能让每一位学生接受的方法，优化出不同学生所能接受的不同方法，优化出适合不同教学内容的方法。教师教学时关注课堂的精彩，更要关注精彩背后的差异化教学方式；关注精彩的课堂，更要关注现实的课外生活。