教育心理学研究指出学生思维的深刻性是学生对具体数学材料进行概括，对具体数量关系和空间形式进行抽象，以及在推理过程中思考的广度、深度、难度和严谨性水平的集中反映。一个数学思维灵活性水平高的学生，思维流畅，富于联想，具备求异思维和求同思维，解答方法的选择合理恰当。培养学生思维的深刻性与灵活性对学生数学能力与品质的发展有着重要的作用。《数学课程标准》强调要发展学生的空间观念、数感和符号感。这三个目标之间并非独立的，而是一个互相联系、相辅相成、密不可分的统一体。教师在教学活动中应引导学生全面、深入、从准、从细地思考问题，抓住事物的本质、规律和内在联系，重视它们之间的协调发展，这对培养学生思维的深刻性与灵活性有着独特的意义。本文尝试从四个方面对小学高年级学生空间观念、数感和符号感协调发展作出初步探析。
     一、 利用直观几何图形演绎数学性质和规律
     用几何图形解释计算公式和变化规律，把抽象的数学式子（算式、代数式）给予几何意义的想象解释。例如学生在初学乘法分配律时都经历：举例——感知——验证——判断——抽象——概念这样一个思维过程，学生虽然能从大量的数学实例中抽象概括出运算定律，但还不能进行数学上的论证。对高年级学生而言，他们不仅具备直观形象思维能力，且抽象逻辑能力也发展到一定水平，因此我们可以通过下面的教学活动将这一运算定律加以解释和论证。
     要求：用字母将由两个小长方形拼成的大长方形的面积表示出来：
     学生思考后能较快发现大长方形的面积两种表示方法。
     1）大长方形的面积=a (b+c)
     2）大长方形的面积=ab+ac
     综合分析1、2得出：a(b+c)=ab+ac请学生积极思考“这个结论它实质是我们以前学过的什么运算定律？”由于学生参于了规律揭示的过程，思维水平有了一个跃进，讨论异常活跃：“这不就是乘法分配律吗？”“乘法分配律原来还可以这样表示！”“我学会了证明乘法分配律！”……
     类似的我们还可以借助现代多媒体教学手段将下面的这些运算定律展示给学生。
     1. a+b+c=a+(b+c)
          a          b         c   
     多媒体演示：一、依次闪动线段a、b、c合并；二、依次闪动线段b、c、a合并。
     2. a+b=b+a            a         b 
     多媒体演示：小球从不同方向滚动经过的距离相等。            
     二、 通过数学性质和规律解决平面图形问题
     在小学生数学能力中，利用已有的知识经验解决实际问题是数学教学活动中一个重要目标，也最能体现学生思维的灵活性。我们运用数学知识中一些性质和规律在解决几何形体问题时，往往可以化难为易、化繁为简。例如对“相等的两个数若同时减去（或加上）一个数，所得的差（或和）也相等”这一条数学性质，小学高年级学生因已储备了大量数学经验，都能理解也能举出许多实例。为发展它们的符号感，我们用字母把它抽象概括出来“若a=b,则a-c=b-c或a+c =b+c”让学生在理解每一个字母的含义的基础之上解题。         
     三、 建立平面图形转换与数学符号之间的对应关系
     培养数感、符号感和空间观念，发展学生思维能力，动手实践、自主探索、合作交流是最有效的学习方式。我们在教学平行四边形面积公式的推导时，会组织学生开展小组活动，把平行四边形剪拼成他们已有的知识经验——长方形。
     总结学生在实践活动中的剪拼方法可分成如下两类：（如图）

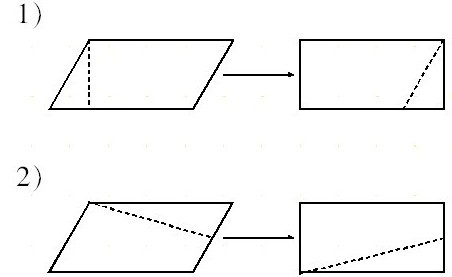
     分析原来的平行四边形与拼成的长方形之间的关系，推导出平行四边形的面积计算公式：S=a×h
     四、借助直观图形展示数概念之间的关系
     如果说数学教学是思维的过程，那概念则是思维的细胞，它是空间形式和数量关系，以及它们的本质属性在人思维中的反映，学生对概念知识的理解与应用是体现学生思维深刻性与灵活性的重要尺度。概念也是数、形、符号的抽象概括，单纯的精讲，学生对问题的本质很难有深刻全面的理解，借助图形、表格等直观形象，学生不但可以形成正确认识，而且能够沟通知识间纵向与横向的联系。
     例如在“数的整除”单元复习时出示导入题“根据1、2、3、4、5、6、7、9、12、24、25、30这些数，用本单元知识说一句话？”学生在打开思路后，教师通过多媒体，把他们提到的相关概念名称“约数、整除、质数……”展现在投影幕上，这时概念显得较杂乱。
     组织学生小组合作操作学习工具（要求：重新排列出让人可以清晰看出概念之间关系的图形）。
     学生在操作中有时为了一个概念位置的摆放而争论不休，思维活跃异常，得到的图形也多种多样。
     在这样的教学活动中，学生借助直观图形表示出概念之间的关系，揭示概念之间的内在联系与本质区别，形成良好的认知，构成了知识网，提高了学生思维的深刻与灵活，促进了学生空间观念、数感和符号感协调发展。
     小学生高年级阶段是学生思维由具体形象到抽象逻辑重要过渡的时期，训练学生思维的深刻性与灵活性显出其独特的作用，在这一时期学生的空间观念、数感和符号感也在同步发展，并互相促进、互相制约。教师在教学活动中应将这三者有机结合，注意知识的连贯性，深入剖析、挖掘其中内在联系，只有这样才能真正培养学生思维的深刻性与灵活性，提高学生思维品质和数学能力。