教育心理学研究指出，学生思维的深刻性是学生对具体数学材料进行概括，对具体数量关系和空间形式进行抽象，以及在推理过程中思考的广度、深度、难度和严谨性的集中反映。《数学课程标准》强调要发展学生的空间观念、数感和符号感，这三个目标是相辅相成、密不可分的统一体。教师在教学活动中引导学生深入地思考问题，抓住事物的本质、规律和内在联系，这对培养学生思维的深刻性与灵活性有着独特的意义。
    一、利用直观几何图形演绎数学性质和规律
    用几何图形解释计算公式和变化规律，把抽象的数学式子（算式、代数式）给予几何意义的想象解释。在教学活动中，利用学生已有的空间观念去深化学生对数感和符号感的认识，揭示抽象的数学性质和规律，这样思维的深刻性与灵活性才能得到培育和发展。
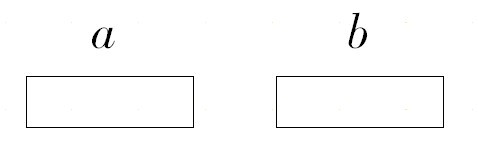
    例如：要求用字母将由两个小长方形拼成的大长方形的面积表示出来：
    学生思考后很快发现大长方形的面积有两种表示方法：
    1.大长方形的面积=a(b+c)
    2.大长方形的面积=ab+ac
    综合分析1、2得出：a(b+c)=ab+ac
    我让学生思考“这个结论是我们以前学过的什么运算定律？”
    由于学生参与了规律揭示的过程，思维一下活跃起来：“这不就是乘法分配律吗？”
    类似的运算定律我们还可以借助现代多媒体教学手段来进行展示。
    例如：              a              b
    a×b=b×a                                        
    多媒体演示：一、闪动a平移；二、闪动b平移；三、比较两次平移的结果。
    二、通过数学性质和规律解决平面图形问题
    在小学生数学能力中，利用已有的知识经验解决实际问题是数学教学活动中的一个重要目标，也最能体现学生思维的灵活性。我们运用数学知识中的一些性质和规律在解决几何形体问题时，往往可以化难为易、化繁为简。例如对“相等的两个数若同时减去（或加上）一个数，所得的差（或和）也相等”这一条数学性质，小学高年级学生因为已储备了大量数学经验，都能理解也能举出许多实例。为发展它们的符号感，我们用字母把它抽象概括出来“若a=b,则a-c=b-c或a+c=b+c”。
    我们的教学不能仅停留在问题的求解上，应适时引导“本题的解答实际上运用了什么数学知识？”，从而沟通数学性质与几何形体之间的关系，提高学生的思维灵活性，训练他们思维的深刻性。
    三、建立平面图形转换与数学符号之间的对应关系
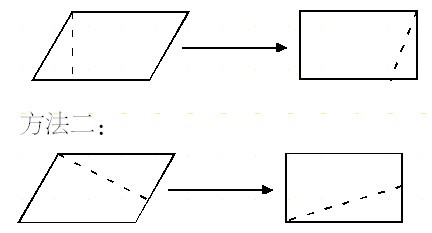
    要培养学生的数感、符号感和空间观念，发展他们的思维能力，动手实践、自主探索、合作交流是最有效的学习方式。我们在教学平行四边形面积公式的推导时，会组织学生开展小组活动，把平行四边形剪拼成他们已有的知识经验——长方形。
    总结学生在实践活动中的剪拼方法可分成两类：
    方法一：

    方法二：

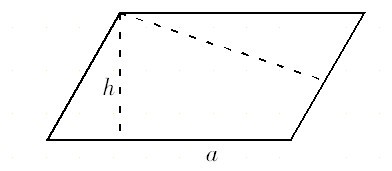
    分析原来的平行四边形与拼成的长方形之间的关系，推导出平行四边形的面积计算公式：S=a×h

    在解题过程中还能得到等式：a×b=c×d。教师在评析过程中往往只注意到a×b和c×d都表示这一个平行四边形的面积，只对等式的合理性作出解释，未能对教材作进一步深入分析，从而找到其中能促进学生思维深刻性与灵活性发展的结合点。若能引导学生在观察平行四边形两类剪拼方法后，在头脑中建立a×b与剪拼方法一，c×d与剪拼方法二之间的对应关系，将对促进学生空间观念、数感和符号感的协调发展大有裨益。
    四、借助直观图形展示数学概念之间的关系
    如果说数学教学是思维的过程，那概念则是思维的细胞，学生对概念知识的理解与应用，体现了学生思维的深刻性与灵活性的重要尺度。概念也是数、形、符号的抽象概括，借助图形、表格等直观形象，可以帮助学生沟通知识间纵向与横向的联系。学生在操作教具时，思维也异常活跃。
    小学高年级阶段是学生的思维由具体形象思维到抽象逻辑思维的重要过渡时期，在这一时期学生的空间观念、数感和符号感也在同步发展，教师在教学活动中只有将这三者有机结合起来，注意知识的连贯性，才能真正培养学生思维的深刻性与灵活性，提高学生的思维品质和数学能力。