《江苏科技报·教育周刊》(双周刊,国内统一刊号CN32-0019),是江苏省唯一以社会立场透析当代中国教育的报纸。秉承“科技推动教育,教育改变人生”的理念,《江苏科技报·教育周刊》一直注意保持与教育前沿工作的密切联系,定位于教育宏观研究,兼顾微观探讨,注重教育文化生态的构建与引导,时刻关注鲜活的教育实态,着眼于教育文化的深层构建,努力赋予教育以深厚的文化内涵,致力打造中国最好的教育媒体。
国内统一刊号:CN32—0019
编辑部地址:江苏省南京市鼓楼区中山路55号新华大厦48楼
| 导学案问题设计之我见 |
| 来源:本站原创 作者:鹤壁市第四中学 王静 发布日期:2019-04-22 10:13:12 |
|
导学案是将静态教材进行动态开发使用,注重把教材的知识转化为一系列有待解决的问题呈现给学生,引导学生通过问题来学习教材,培养和提高学生学习、探索、创新等综合能力,其设计核心就是对教学内容问题化的设计。通过不断探索和总结,我认为在导学案的问题设计过程中应遵循以下基本要求。
教材是学生学习的媒介,导学案的问题设计必须深入研究教材,紧紧围绕“四基”目标要求,提炼知识脉络,把握重点,找准关键点。问题应围绕学习目标来设计,充分体现“四基”目标的落实,不能“跑偏”,适度性原则主要在于难度的把握上,问题设计过难,不仅问题不能得到有效解决,还会让学生自信心受挫,失去学习的动力;问题设计过简,在解决过程中没有任何障碍,学生的思维挑战没有得到满足,解决问题的积极性受到打击。所以导学案要结合学生的实际情况,设定适度的问题导向。 例如在设计“有理数乘法”导学案中,我设计了如下问题。
同号两数相乘:(-3)×(-1)=3;(-3)×(-2)=6;(-3)×(-3)=9。 观察以上两级算式,回答下列问题:积的正负号与因数的正负号有什么关联?积的绝对值与因数的绝对值有什么关联?对比两组结果,如果把一个因数换成它的相反数,所得的积会发生什么变化?归纳总结有理数的乘法法则。 在学生学习掌握有理数乘法法则的基础上,我又进一步设计了一个拓展提升问题:假设a、b为有理数,那么——
若ab<0,a+b>0,|a|>|b|,则a、b的符号怎样? 该问题的设置充分考虑学生在有理数乘法运算中符号掌握难的特点,对基础知识进行巩固提升的同时,实现对教学难点的突破。 二、问题的设计要具有情境性 建构主义学习理论认为,应重视创设学习情境,尽可能提供“真实”的、“生活”的学习情境和活动。为更好地激发学生的学习兴趣,我经常在教学中选择一些源于生活、超越常规但又在情理之中且具有一定挑战性的生活情境,设计成问题来激发学生探究的兴趣。问题情境的来源,可以是已有的经验、生活和生产实际、与数学有关的社会热点问题、科学技术的发展前沿、数学史实等多个方面。 例如在设计“幂的乘方”导学案时,我结合电影《流浪地球》设计了如下问题。
木星的半径大约是地球半径的10倍,太阳的半径大约是地球半径的102倍,假如地球的半径为r,那么太阳和木星的体积分别是多少?(球的体积公式为 这些问题使学生更加理解所学内容的生活意义和社会意义,学会利用书本知识解决生活中的实际问题,培养学生的学科素养,进一步落实“四基”目标。 三、问题设计要注重层次化、递变性
在学习一次函数与一元一次方程、一元一次不等式关系时,知识点较抽象,难度较大。我在设计导学案时就进行了层次分解,尽量让抽象知识更加直观。
求-2x+3=0的解___,它是点(__,__)的横坐标; 求-2x+3=2的解___,它是点(__,__)的横坐标;
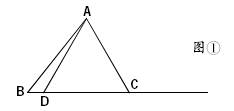
让学生从一次函数图像中发现一元一次方程的解、一元一次不等式的解集,引导学生对“数”从“形”的角度进行思考,真正理解两者之间的联系,初步感受研究方程与函数关系的方法,积累研究活动经验。 对难度较大的问题还可进行层次分解,降低难度。在学习“全等三角形的判定(边角边)”时,在探讨“两边及其一边所对的角对应相等的两个三角形全等”是假命题时,学生想象反例图形时有困难,我设计了一系列问题帮助学生实现探究。如图①:作△ABC使AB>AC。以点A为圆心、线段AC长为半径作弧,交BC于点D得到△ABD。观察:△ABC和△ABD有哪些相等的元素?它们全等吗?为什么?你得出什么结论?
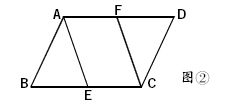
注重学习的递变性,在教学中为学生设计一些变式训练,一题多变,由易到难逐步进行,提高学生的解题灵活性和对知识的巩固提升。 例如在学习定理“一组对边平行且相等的四边形是平行四边形”时,我设计了如下几个问题。
变式训练1:在平行四边形ABCD中,E、F分别是对边BC和AD上的两点,且BE=FD,求证:四边形AECF为平行四边形。
让学生感受在图形不变时,已知条件发生改变时定理的不同使用,实现定理的灵活应用,完成教学目标。 四、问题的设计要具有开放性 开放的问题通常会有多个备选答案,要求学生提出多个可供选择的解决方案,每个方案都有自己的优势和劣势。设置开放性问题,目的就是转变学生的思维习惯和思维定式,激活学生的求异思维和创新思维。设计问题时既要注重问题的开放性价值,又要在学习目标的指导下,给学生适当的引导,提高课堂学习效率。
身高为1.6m的小明直立于旗杆影子的顶端处,测得同一时刻自己和旗杆的影子长分别为1.2m、9m,则旗杆的高度为_______m。 设学校操场上的旗杆的仰视目光与水平线的夹角为58°,观测点距旗杆为5m,请利用比例尺构造一个与实物相似的三角形,画出简图并测量简图中对应线段长度,计算学校旗杆高度。 通过这些问题的解决,引导学生总结已学习的测量知识,学习设计测量方案解决实际问题,同时为后续三角函数的学习打下基础。 |
| 发表评论 |

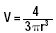 )
)